0. 前言
- 目标:自己写代码实现双线性插值,并能讲出道理来。
- 参考资料:
1. 线性插值
- 维基百科配图如下:
- 加上一点自己的理解:不能直接用于图像插值,毕竟这个只能补全一条对角线上的值。
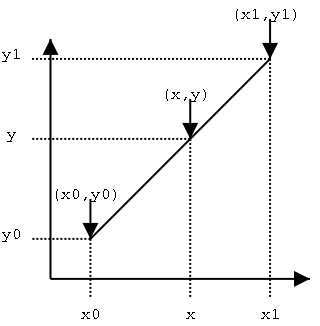
- 要解决的问题:
- 已知
(x0, y0)和(x1, y1),以及(x,y)中的一个值。 - 即使用
x, x0, y0, x1, y1计算y或使用y, x0, y0, x1, y1计算x。 - 计算公式很容易,将上面的参数带入下面公式即可:$$\frac{y-y_0}{x-x_0} = \frac{y_1-y_0}{x_1-x_0}$$
- 已知
- 应用举例:
- 假设一个表格列出了一个国家 1970年、1980年、1990年以及 2000年的人口,那么如果需要估计 1994年的人口的话,线性插值就是一种简便的方法。
- 可以通过三步线性插值完成一次双线性插值运算。
2. 双线性插值
2.1. 理论介绍
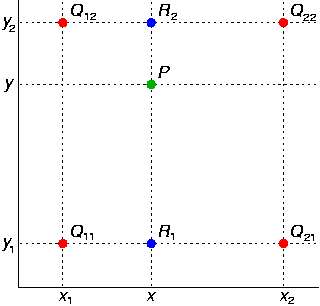
- 维基百科配图如下:
- 加上一点自己的理解:
- 不仅要知道
x1, x2, y1, y2, x, y的取值,还需要知道Q11, Q12, Q21, Q22的取值。 - 先经过线性插值计算
R1, R2的取值,再通过线性插值计算P的取值。 - 即,双线性插值是通过三次线性插值获取。
- 不仅要知道
- 加上一点自己的理解:
- 要解决的问题:
- 假设像素值的函数为
f(x, y) - 在已知
x1, x2, y1, y2以及Q11, Q12, Q21, Q22四个位置像素值的前提下,计算$(x, y), x \in [x_0, x_1], y \in [y_0, y1]$处的取值。 - 假设
Q11, Q12, Q21, Q22四个位置像素值为f(Q11), f(Q12), f(Q21), f(Q22)。 - 从图像插值的角度看,
x, y, x1, y1, x2, y2都是像素的坐标位置,Q11, Q12, Q21, Q22是四个位置对应的坐标,f(Q11), f(Q12), f(Q21), f(Q22)为对应的像素值,要计算(x, y)的是像素值。
- 假设像素值的函数为
- 具体过程:
- 首先对x轴方向进行线性插值:
- $$R_1 = f(x, y_1) \approx \frac{x_2-x}{x_2-x_1}f(Q_{11}) + \frac{x_2-x}{x_2-x_1}f(Q_{21}) $$
- $$R_2 = f(x, y_1) \approx \frac{x_2-x}{x_2-x_1}f(Q_{12}) + \frac{x_2-x}{x_2-x_1}f(Q_{22}) $$
- 再通过
R1, R2计算线性插值,获取P的结果:- $$f(x, y) \approx \frac{y_2-y}{y_2-y_1} R_1 + \frac{y-y_1}{y_2-y_1} R2$$
- 先从y轴、再从x轴进行线性插值的结果是一样的。
- 首先对x轴方向进行线性插值:
2.2. 具体实现介绍
- 具体实现描述:
- 假设初始图片为
img1,尺寸为h,w,像素点坐标作为记作 $(x_i, y_i)$。 - 假设目标图像
img2,图像尺寸为hh, ww,像素点坐标记作 $(xx_i, yy_i)$。 - 双线性插值的目标是以
img1作为输入,获取图像img2。
- 假设初始图片为
- 实现步骤:
- 找到目标图像
img2中每个像素点 $(xx_i, yy_i)$对应于原始图像中的位置,记作 $(x_i’, y_i’)$ - $(x_i’, y_i’)$ 就是
2.1.配图中点P的位置。 - 通过
ceil/floor操作获取Q11, Q12, Q21, Q22对应的坐标值。 - 之后就可以通过
2.1.中的双线性插值的具体过程获取对应点像素值。
- 找到目标图像
- 实现的重点与难点:就是上述实现步骤一,获取目标图像中每个像素点对应于原始图像中的坐标。
- 根据比例获取对应坐标:
- 根据上面的假设,可以获得两个比例 $scale_h = h/hh, scale_w = w/ww$。
- 那么对于目标图像中每一个坐标 $(xx_i, yy_i)$ 就对应于原始图像中的:$x_i’ = scale_h * xx_i, y_i’ = scale_w * yy_i$
- 这样做存在的问题:实现过程中,所有坐标都是从0开始编号的,这就会导致有偏移。
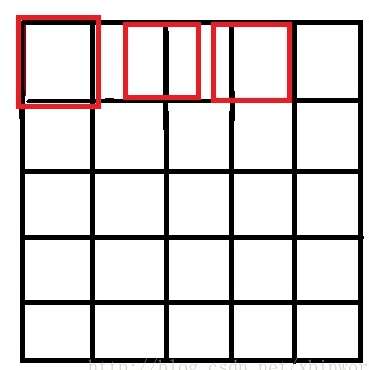
- 举个例子,如果想把
5*5的图像转换为3*3,那么最终得到的三个横坐标分别是0, 5/3, 10/3,很显然,这结果偏移到左边了。这个结果,也就是很多博客中提到的配图(注意下图中的横坐标):
- 为了解决根据比例获取对应坐标存在的问题,cv2等库都使用了中心对齐获取坐标。
- 从实现角度看很简单,将原本的转换公式 $x_i’ = scale_h * xx_i, y_i’ = scale_w * yy_i$ 稍微修改一下。
- 改成:$x_i’ = scale_h * (xx_i + 0.5) - 0.5, y_i’ = scale_w * (yy_i + 0.5) - 0.5$