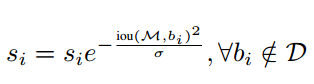小白填坑系列(5) NMS & Soft NMS

发表于 | 分类于 ， ，
字数统计: 1k | 阅读时长 ≈ 4
NMS与Soft NMS的简单理解

0. 前言

  • NMS，全称 non-maximum suppression，中文翻译是非极大值抑制。

1. NMS的引入与基本流程

1.1. 引入

  • 检测模型获取得到的检测框一般较多，同一物体很可能有多个框选中，所以就需要筛选一些。
  • 筛选的方法主要有两种，一种是通过增加 score 阈值，另一种就是NMS。
  • NMS的总体思路就是 从一些类似的候选框中选择一个最好的。
    • 类似的候选框指的是两个bbox的IOU大于某一阈值。
    • 好的候选框指的是score高的。
  • 检测的基本流程
    • 参考本文的配图（这张图多个博客引用了，我也不知道最开始从哪里引用的）：
      • image_1dqf0qbpou2j10qj11pi1pss16569.png-467.1kB
    • 第一步：对每一类型，根据socre降序排列所有候选框。
    • 第二步：以第一步结果作为输入，依次遍历每个候选框，若后续候选框中有与当前候选框的IOU大于阈值，则剔除对应后续候选框中的对象。重复该操作，直到遍历过所有候选框。
    • 第三步：剩下的候选框，就是NMS的结果。

1.2. 基本实现

  • 参考：rgbirshick/py-faster-rcnn: lib/nms，即RGB大佬的NMS实现
  • 基本流程
    • 第一步：将检测出的bbox按照cls score划分为若干集合。
    • 第二步：对每个集合，按照cls score排列，得到一个降序的list_k。
    • 第三步：对每个list_k，从top 1 cls score开始，计算当前bbox_a与其他bbox_b的IOU，若IOU大于阈值则去除bbox_b，且最终保留bbox_a，并从list_k中剔除。
    • 第四步：从list_k中选择剩余的top 1bbox，按照第三步的方法继续进行筛选。
    • 第五步：对所有list_k进行相同的操作。
  • 源码
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    def nms(dets, thresh):
        x1 = dets[:, 0]
        y1 = dets[:, 1]
        x2 = dets[:, 2]
        y2 = dets[:, 3]
        scores = dets[:, 4]
        areas = (x2 - x1 + 1) * (y2 - y1 + 1)
        order = scores.argsort()[::-1]
        keep = []
        while order.size > 0:
            i = order[0]
            keep.append(i)
            xx1 = np.maximum(x1[i], x1[order[1:]])
            yy1 = np.maximum(y1[i], y1[order[1:]])
            xx2 = np.minimum(x2[i], x2[order[1:]])
            yy2 = np.minimum(y2[i], y2[order[1:]]）
            w = np.maximum(0.0, xx2 - xx1 + 1)
            h = np.maximum(0.0, yy2 - yy1 + 1)
            inter = w * h
            ovr = inter / (areas[i] + areas[order[1:]] - inter)
            inds = np.where(ovr <= thresh)[0]
            order = order[inds + 1]
        return keep

1.3. 不使用排序实现

  • 本文介绍了不使用排序实现NMS的过程。
  • 其实本质上来说，NMS做的就是去掉重复的候选框。
  • 基本步骤：
    • 第一步：依次遍历所有候选框。
      • 第二步：计算当前候选框（记作候选框A）与剩下候选框的IOU，选出IOU大于阈值的候选框集合（记作候选框集合B）。
      • 第三步：如果候选框A的score比候选框集合B中所有的都大，那就保留候选框A，并去掉所有候选框集合B中元素。
      • 第四步：若候选框集合B中有元素的score大于候选框A的score，则去除候选框A。

2. Soft NMS

2.1. 引入与理解

  • NMS存在一个问题，如果两个同类物体离得太近（即两个同类物体的 gt bbox 本身的IOU就大于阈值），那就只能检测到一个物体。
  • image_1dto68fu4erv1gck1v341p1svdm.png-619.2kB
  • 理解：
    • 普通NMS的做法是，当两个bbox的IOU大于一定阈值，则会过滤掉score较小的bbox。
    • Soft NMS的做法是，当两个bbox的IOU大于一定阈值，score较大的bbox的score保持不变，较小的bbox的score会根据一定的方式减少。
    • 普通NMS可以理解为：
      • image_1dto6a3ns19prqsc1b1a14t21qno13.png-14.3kB
    • Soft NMS 可以理解为：
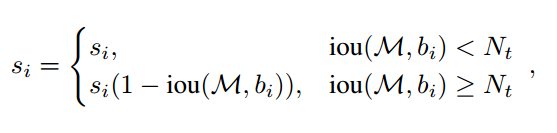
      • image_1dto6bcc017rfe75f23hjhep21g.png-18.7kB
      • 当然，$s_i(1-iou(M, b_i))$ 也可以通过别的方式
        • image_1dto6d8mkuran0e10vn17f23eo1t.png-7.1kB

2.2. 伪代码

  • 引用了这篇文章中的配图
  • 注意，我觉得伪代码里少了一步，就是根据socre threshold来筛选bbox（否则感觉并没有筛选bbox，而只是修改了score）
  • image_1dto5tiq98sf15e5gjd1i3n1em9.png-571.5kB